Martin Sera
Junior Associate Professor, Doctor of Natural Science
- sera.martin

- Website
- https://researchmap.jp/msera
- Areas of Research
- Mathematics, Complex Analysis, Complex Geometry
- Profile
- Research
-
In 2010, Dr. Martin Sera graduated from the Department of Mathematics at the University of Wuppertal, Germany and obtained his Ph.D. from the same institution in 2015. After a one-year postdoctoral in Wuppertal, he received a grant from the German Research Foundation (DFG) to work as a postdoctoral guest researcher at the Department of Mathematical Sciences at Chalmers University of Technology and the University of Gothenburg in Sweden for one year. Supported by the Knut and Alice Wallenberg Foundation, he continued working as a postdoctoral research assistant in Gothenburg for two additional years.
Dr. Sera specialize in complex analysis. The field of complex analysis plays a vital role in mathematics. It is connected to and applied in various fields such as differential geometry, number theory, or theoretical physics. An especially interesting part of complex analysis is the subfield of complex geometry: the study of complex manifolds as they are used in string theory for instance. While smooth manifolds are already quite thoroughly studied, only little is known in the presence of singularities. Therefore, Dr. Sera chose complex geometry with a focus on singularities as his research field. Using L²-Dolbeault cohomologies, he analyzed the geometry of singular complex curves. He continued this work to study singular complex spaces. Furthermore, he used coherent sheaves to classify their singularities. Recently, he has dedicated himself to studying singular Hermitian metrics on vector bundles in detail. As a crucial tool, he applies generalized Monge-Ampère products to define the wedge product of currents related to the curvature.
In his spare time, Dr. Sera enjoys taking pictures. To find nice shots, he likes to discover interesting cities and various places.
-
Geometry Understood Using Curvature and Metrics
When we look around us, we do not really see that the earth is round. Yet, it is easy to see when viewed on a larger scale. Let us take a triangle on the surface of the earth (without hills and valleys) and sum up the angles between its edges. If we measure carefully enough (or if the triangle is very big), we see that the sum of the angles is strictly greater than 180°. Did we not learn in school that the sum is always 180°? Indeed, this is the case for all triangles in the plane. Ergo, the surface of the earth cannot be flat like a plane. To be more general, we see that the geometry of a sphere, the surface of a ball, is encoded in parameters as the sum of angles of triangles. The mathematical concept behind this is curvature. The plane has no curvature, and is flat. The sphere has curvature. Surfaces like spheres are called elliptic. Their so-called Gauß-curvature is positive. Are there also triangles where the sum of the angles is less than 180°? Yes, triangles on surfaces like a saddle have this property (as for the third object in the picture). Such surfaces are called hyperbolic, their Gauß-curvature is negative.
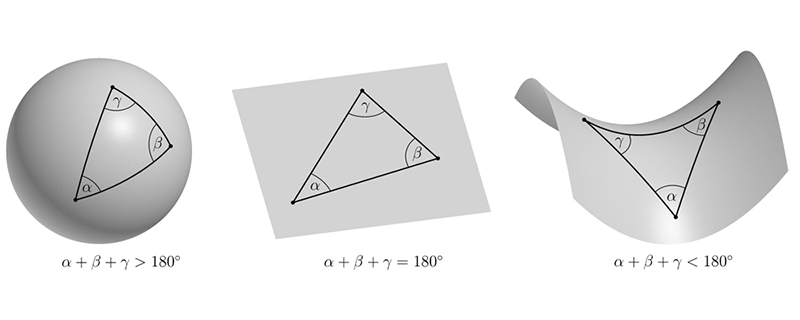
The Gauß-curvature gives a quite comprehensive understanding of the geometry of surfaces. When considering more complicated objects, for instance, of higher dimension, we have to use different tools generalizing the concept of curvature. Interested in the geometry of so-called complex manifolds, Dr. Sera and his collaborators from Germany, Sweden and Japan are studying singular Hermitian metrics on holomorphic vector bundles. A Hermitian metric can be seen as a generalization of measuring length and angles. They are very useful for computing parameters representing the manifold’s curvature.Unfortunately, this works only for special kinds of metrics which do not exist on all complex manifolds. By considering metrics with singular behavior, Dr. Sera and his collaborators are able to apply such computations to a much wider range of manifolds than ever considered before.